Недавно я задумался о парадоксе Монти Холла — той самой задаче с тремя дверями, где нужно угадать, за какой из приз, и потом решить, менять выбор или нет.
На YouTube полно роликов, где объясняют, почему смена выбора увеличивает шансы с 1/3 до 2/3. Казалось бы, всё просто, но если заглянуть в комментарии к этим видео, там творится настоящее побоище! Люди спорят, приводят свои теории, отказываются верить математике — кто-то даже пишет, что это ‘обман’ или ‘ловушка’.
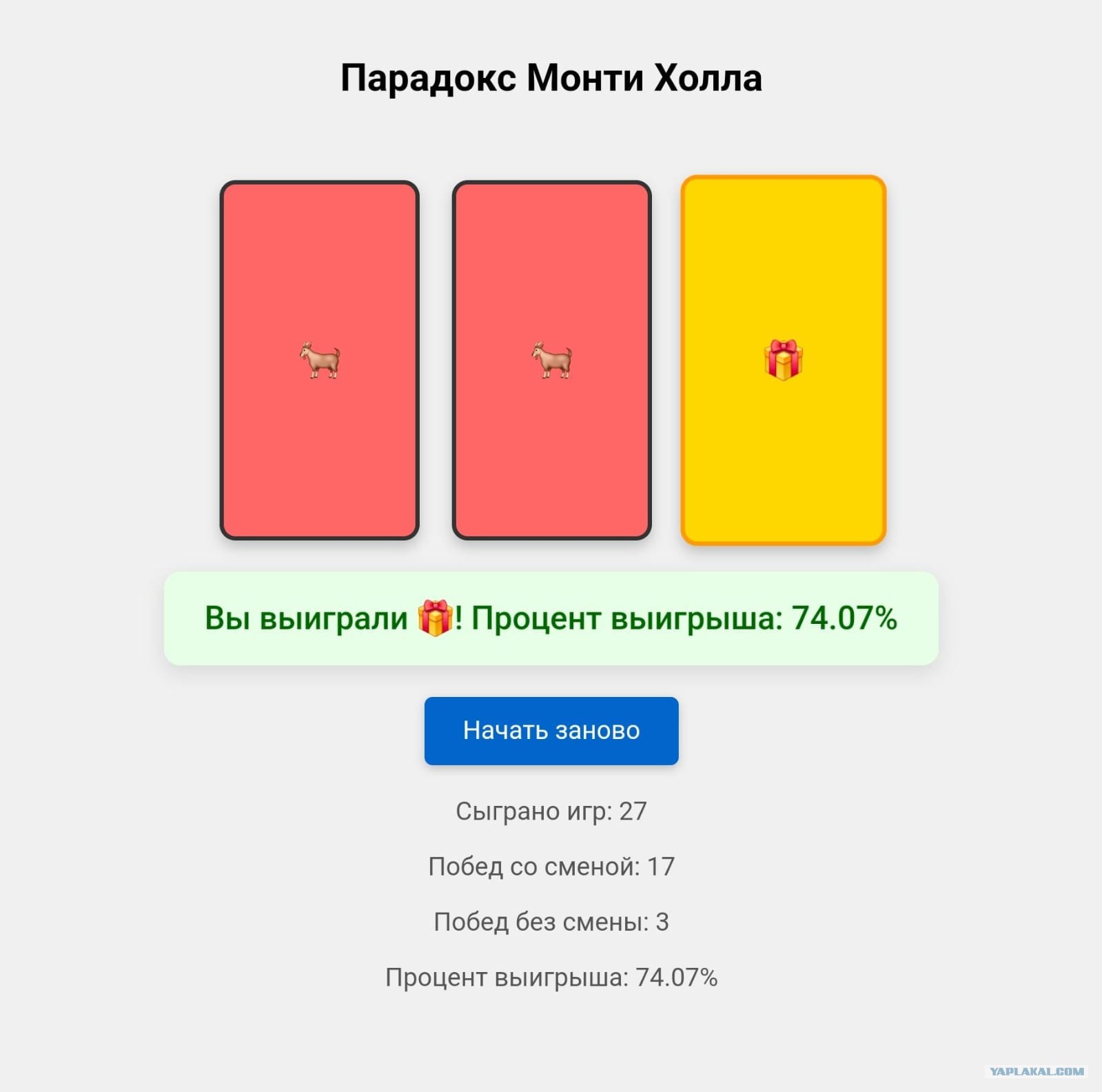
Мне стало любопытно, и я решил проверить всё сам. Написал небольшую программу: она случайным образом прячет приз за одной из трёх дверей, даёт выбрать дверь, потом ‘ведущий’ открывает пустую, и можно либо остаться при своём выборе, либо поменять его.
Статистика — и да… программа ведет статистику по всем попыткам. И знаете что? Всё сходится! Если не менять выбор, выигрыш — в 33% случаев, а если МЕНЯТЬ — около 66%. То есть всё, как говорят ютуберы.
В общем, парадокс Монти Холла — это не просто задачка, а ещё и тест на то, как мы воспринимаем вероятности. А вы что думаете? Пробовали сами проверить?
Можно провести эксперимент: сыграть 20 раз, не меняя выбор, потом ещё 20 раз, всегда меняя выбор, и сравнить результаты.
Проверить можно здесь